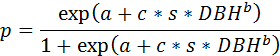Windstorm

Windstorm kills trees due to storm events.

Trees removed by this behavior will have a mortality reason code of "storm".

Parameters for this behavior

Parameter name	Description
Windstorm - DBH Exponent (b)	The "b" value in the equation used to determine the mortality of an individual tree as a result of a storm.
Windstorm - Minimum DBH for Windstorm Mortality	The minimum DBH for trees to be killed in storm events.
Windstorm - Mortality Intercept (a)	The "a" value in the equation used to determine the mortality of an individual tree as a result of a storm.
Windstorm - Sea Surface Temperature Cyclicity Period (Years)	Parameter that controls the cyclicity of storm frequency. This value cannot be 0.
Windstorm - Severity for 1 Year Return Interval Storm	The severity of storms with a 1 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 5 Year Return Interval Storm	The severity of storms with a 5 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 10 Year Return Interval Storm	The severity of storms with a 10 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 20 Year Return Interval Storm	The severity of storms with a 20 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 40 Year Return Interval Storm	The severity of storms with a 40 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 80 Year Return Interval Storm	The severity of storms with a 80 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 160 Year Return Interval Storm	The severity of storms with a 160 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 320 Year Return Interval Storm	The severity of storms with a 320 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 640 Year Return Interval Storm	The severity of storms with a 640 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 1280 Year Return Interval Storm	The severity of storms with a 1280 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Severity for 2560 Year Return Interval Storm	The severity of storms with a 2560 year return interval, as a value between 0 (no mortality) and 1 (complete devastation).
Windstorm - Storm Cyclicity Sine Curve d	Parameter that controls the cyclicity of storm frequency. For no cyclicity, set this value to 0. This value is part of the sine curve term and controls the sine amplitude.
Windstorm - Storm Cyclicity Sine Curve f	Parameter that controls the cyclicity of storm frequency. This value is part of the sine curve term and controls the sine frequency.
Windstorm - Storm Cyclicity Sine Curve g	Parameter that controls the cyclicity of storm frequency. This value is part of the sine curve term and controls where on the sine curve storms start occurring.
Windstorm - Storm Cyclicity Trend Function Intercept (i)	Parameter that controls the trend of cyclicity of storm frequency. This value is part of the trend term and is the intercept of the function controlling the increase or decrease of overall frequency cycling. For no cyclicity at all, set this term to 1. For no trend in cyclicity, set this term to 0.
Windstorm - Storm Cyclicity Trend Function Slope (m)	Parameter that controls the trend of cyclicity of storm frequency. This value is part of the trend term and is the slope at which frequency cycling increases or decreases. For no cyclicity, or no trend in cyclicity, set this term to 0.
Windstorm - Storm Intensity Coefficient (c)	The "c" value in the equation used to determine the mortality of an individual tree as a result of a storm.
Windstorm - Timestep to Start Storms	The first timestep that storms are allowed to occur.

How it works

Using the parameters, you provide a general "shape" of storm intensity. SORTIE then decides which storms occur each timestep, and which trees die as a result.

This behavior defines 11 storm return intervals: 1, 5, 10, 20, 40, 80, 160, 320, 640, 1280, and 2560 years. Each has a set annual probability: for example, an 80-year return interval storm has an annual probability of 1/80, or 0.0125. For each year of each timestep, for each return interval, SORTIE generates a random number to decide whether a storm of that return interval will occur. This means that there can be multiple storms in a timestep, or no storms at all. In a multi-year timestep, a storm of a given return interval can happen more than once.

You give each return interval a storm severity value, between 0 and 1. These are defined in the Windstorm - Severity for X Year Return Interval Storm parameters. A severity of 0 means no tree mortality; a severity of 1 approaches 100% mortality.

The overall frequency of storms can remain constant, or it can change through time. It has been reported in Goldenburg et al 2001 that storm activity in the North Atlantic cycles along with sea surface temperature. This behavior can thus change the storm frequency over time, using either a sinusoidal pattern, a constant linear change, or both together. In the figure below, curve 1 is a basic sine wave. Curve 2 has a sinusoidal pattern plus an upwards trend.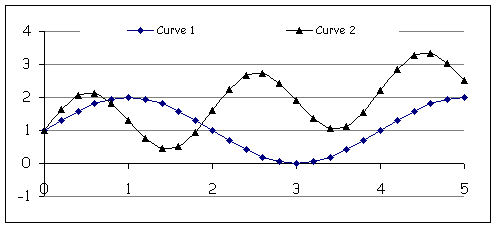

The actual probability of an individual storm that takes place in a storm regime with a cyclical frequency is:

P'(F_i) = P(F_i) * ([d * sin( π * (x-g) / (2f) )] + [mx + i])

Note that the new probability is a baseline probability, P(F_i), multiplied by a value that adjusts the probability according to where the model is at the given time in the frequency cycle. The frequency cycle multiplier is itself made up of two terms added together. The first term is the sine curve cycling, and the second term is the overall trend upwards or downwards.

Terms in the equation:

P'(F_i) is this timestep's annual probability of a storm of the ith return interval, adjusted according to the frequency cyclicity
P(F_i) is the baseline probability of a storm of the ith return interval; that is, the inverse of the values specified in the Windstorm - Severity for X Year Return Interval Storm parameters
x = 4 * t / Sr, where t is the number of years since storms started and Sr is the Windstorm - Sea Surface Temperature Cyclicity Period (Years) parameter
d is the Windstorm - Storm Cyclicity Sine Curve d parameter, which controls the sine curve's amplitude
f is the Windstorm - Storm Cyclicity Sine Curve f parameter, which controls the sine curve's frequency
g is the Windstorm - Storm Cyclicity Sine Curve g parameter, which controls where on the sine curve storms start occurring
m is the Windstorm - Storm Cyclicity Trend Function Slope (m) parameter
i is the Windstorm - Storm Cyclicity Trend Function Intercept (i) parameter

To turn off all cyclicity and use constant storm probabilities, set Windstorm - Storm Cyclicity Sine Curve d to 0, Windstorm - Storm Cyclicity Trend Function Slope (m) to 0, and Windstorm - Storm Cyclicity Trend Function Intercept (i) to 1. (The other values are unimportant.) To use only the sine portion with no trend line, set both Windstorm - Storm Cyclicity Trend Function Slope (m) and Windstorm - Storm Cyclicity Trend Function Intercept (i) to 0. To use only the trend portion, set Windstorm - Storm Cyclicity Sine Curve d to 0.

For each storm that occurs, Windstorm decides what trees will die as a result. A tree's probability of mortality is calculated as follows: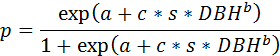

where:

p is the tree's probability of mortality
a is the Windstorm - Mortality Intercept (a) parameter
c is the Windstorm - Storm Intensity Coefficient (c) parameter
b is the Windstorm - DBH Exponent (b) parameter
DBH is the tree's DBH, in cm
s is the storm's severity, set in the parameter for its return interval

Below severity 0.1, the model becomes unreliable; so in that case, the severity is treated as a straight probability of mortality for all trees. For example, if a storm occurs of severity 0.05, all trees have the same 5% chance of dying. If a storm return interval's severity is set to 0, then that storm never occurs.

It is possible for a storm to occur and kill no trees, especially if it is a very mild storm or the forest has no large trees. Unlike the other SORTIE storm behaviors, there is no damaged-but-alive state. After a windstorm a tree is either dead or in perfect health.

Storm events happen "independently". Every time a storm happens, all eligible trees have a separate chance of mortality. Of course, the storms can never truly be independent. A storm can only kill the trees that another storm hasn't already killed.

Trees killed in a windstorm are treated like trees killed in natural mortality. They will form snags if the run uses snags, and are available for processes such as substrate.

Seedlings and snags are never killed by storms. For adults and saplings, only those trees to which the Windstorms behavior has been applied will be considered for storm mortality; and of those trees, only those trees with a DBH larger than the value in the Windstorm - Minimum DBH for Windstorm Mortality parameter can be killed.

You can delay the introduction of windstorms into the run using the Windstorm - Timestep to Start Storms parameter. If this value is greater than 0, no storms will occur until that timestep is reached.

Information on what storms occurred during a run is saved in the Windstorm Results grid. This grid lists how many storms occurred each timestep, and the basal area and density killed of each species in that storm.

How to apply it

Add this behavior to your run and apply it to saplings and/or adults of any species. If you wish to get results on storm events, save the Windstorm Results grid data in a detailed output file. You can then view the contents of this grid as a table using SORTIE's data visualization system.